Numbers and Place Value
What is the difference between a ‘numeral’ and a ‘number’?
A numeral is the symbol, or collection of symbols, that we use to represent a number. The
number is the concept represented by the numeral, and therefore consists of a whole network
of connections between symbols, pictures, language and real-life situations.
The same number (for example, the one we call ‘three hundred and sixty-six’) can be represented by different numerals – such as 366 in our Hindu-Arabic, place-value system, and CCCLXVI using
Roman numerals
Because the Hindu-Arabic system of numeration is now more or less universal, the distinction between the numeral and the number is easily lost.
What are the cardinal and ordinal aspects of number?
cardinal基数;
a number, such as 1, 2 and 3, used to show quantity rather than orderordinal序数词(如第一、第二等)
a number that refers to the position of sth in a series, for example ‘first’, ‘second’, etc.
s an adjective describing a small set
of objects: two brothers, three sweets, five fingers, three blocks, and so on. This idea of a number
being a description of a set of things is called the cardinal aspect of number.
numbers used
as labels to put things in order. For example, they
turn to page 3 in a book.
The numerals and words being used here do not represent
cardinal numbers, because they are not referring to sets of three things.In these examples, ‘three’ is one thing, which is labelled three because of the
position in which it lies in some ordering process. This is called the ordinal aspect of number.
The most important experience of the ordinal aspect of number is when
we represent numbers as locations on a number strip or as points on
a number line

There is a further way in which numerals are used,
sometimes called the nominal aspect. This is where
the numeral is used as a label or a name, without any
ordering implied. The usual example to give here
would be a number 7 bus.
What are natural numbers and integers?
use for
counting: {1, 2, 3, 4, 5, 6, …}, going on forever.
These are what mathematicians choose to call the set
of natural numbers
the set of integers: {…, –5, –4, –3, –2, –1, 0, 1,
2, 3, 4, 5, …} now going on forever in both directions.
includes both positive integers (whole numbers greater than zero) and negative integers (whole
numbers less than zero), and zero itself.
The integer –4 is properly named ‘negative four’,
the integer +4 is named ‘positive four’,
natural numbers are positive integers.

What are rational and real numbers?
include fractions and decimal
numbers (which, as we shall see, are a particular kind of(是一种特殊的) fraction), we get the set ofrational numbers.
The term ‘rational’ derives from the idea that a fraction represents a ratio.
The technical
definition of a rational number is any number that is the ratio of two integers.
Rational numbers enable us to subdivide the
sections of the number line between the integers and to label the points in between,

there are other real numbers that cannot be written down as exact fractions or decimals – and are therefore not rational.
there is no fraction or decimal that is exactly equal to the square root of 50 (written as √50).
This means there is no rational number that when multiplied by itself gives exactly the answer
50.
– we could never get a number
that gave us 50 exactly when we squared it.
But √50 is a real number – in the sense that it
represents a real point on a continuous number line, somewhere between 7 and 8. It represents
a real length. So this is a real length, a real number, but
it is not a rational number. It is called an irrational number.
利用勾股定理得到平方根数的实际长度
the
set of real numbers includes all rational numbers – which include integers, which in turn
include natural numbers – and all irrational numbers.
What is meant by ‘place value’?
in the Hindu-Arabic system
we do not use a symbol representing a hundred to
construct three hundreds: we use a symbol representing three! Just this one symbol is needed to represent
three hundreds, and we know that it represents three
hundreds, rather than three tens or three ones, because
of the place in which it is written.
in our Hindu-Arabic place-value system, all
numbers can be represented using a finite set of digits,
namely, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Like most numeration systems, no doubt because of the availability of
our ten fingers for counting purposes, the system uses
ten as a base.
Larger whole numbers than 9 are constructed using powers of the base: ten, a hundred, a
thousand, and so on.
The place in which a digit is written, then, represents that number of one of these powers
of ten
for example, working from right to left, in the numeral 2345 the 5 represents
5 ones (or units), the 4 represents 4 tens, the 3 represents 3 hundreds and the 2 represents
2 thousands.
the
numeral 2345 is essentially a clever piece of shorthand, condensing a complicated mathematical
expression into four symbols, as follows:
(2 × 103) + (3 × 102) + (4 × 101) + 5 = 2345.
Perversely, we work from right to left in determining the place values, with
increasing powers of ten as we move in this direction. But, since we read from left to right,
the numeral is read with the largest place value first
the principle of exchange.
This means that whenever you have accumulated ten in one place, this can be exchanged for
one in the next place to the left. This principle of being able to ‘exchange one of these for ten
of those’ as you move left to right along the powers of ten, or to ‘exchange ten of these for one
of those’ as you move right to left, is a very significant feature of the place-value system.
This principle of exchanging is also fundamental to the ways we do calculations with
numbers. It is the principle of ‘carrying one’ in addition
It also means that,
when necessary, we can exchange one in any place for ten in the next place on the right, for
example when doing subtraction by decomposition.
It also means that,
when necessary, we can exchange one in any place for ten in the next place on the right, for
example when doing subtraction by decomposition
How does the number line support understanding of place value?
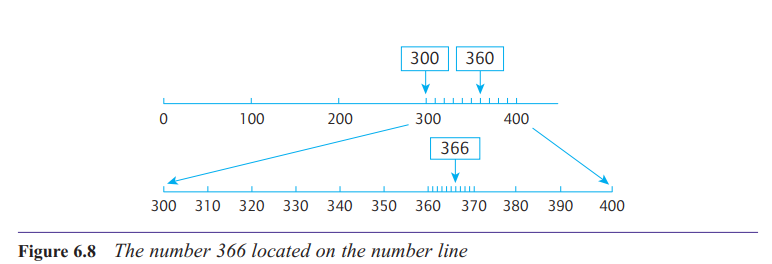
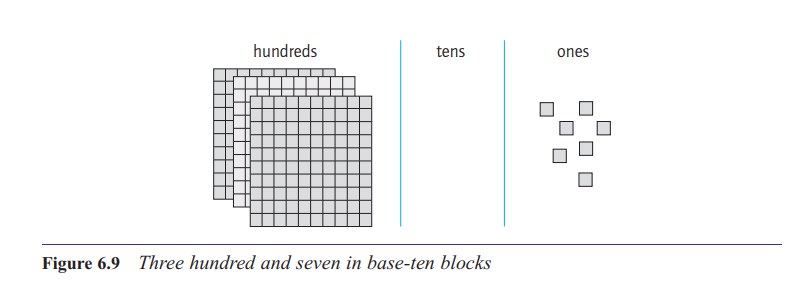
What is meant by saying that zero is a place holder?
‘three hundred and seven’ represented in base-ten blocks. Translated into symbols,
without the use of a zero, this would easily be confused with thirty-seven: 37. The zero is used therefore as a place holder; that is, to indicate the position
of the tens’ place, even though there are no tens
there: 307. It is worth noting, therefore, that when we
see a numeral such as 300, we should not think to
ourselves that the 00 means ‘hundred’.It is the position of the 3 that indicates that it stands for ‘three hundred’; the function of the zeros is to make this
position clear whilst indicating that there are no tens
and no ones.
How is understanding of place value used in ordering numbers?
It
is always the first digit in a numeral that is most significant in determining the size of the number.
A statement that one number is greater than another (for example, 25 is greater than 16) or
less than another (for example, 16 is less than 25) is called an inequality
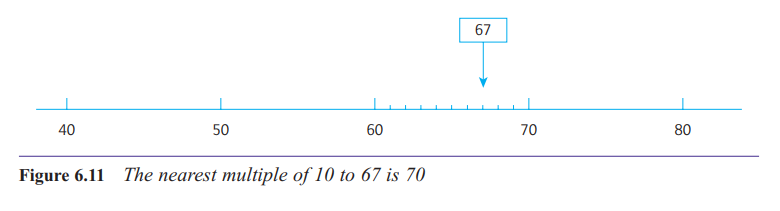
How are numbers rounded to the nearest 10 or the nearest 100?
Rounding is an important skill in handling numbers
One skill to be learnt is to round a number or quantity to the nearest something.
round a 2-digit number to the nearest ten.
67 lies between 60 and 70, but is nearer to 70
Addition and Subtraction Structures
What are the different kinds of situation that primary children might encounter to which the operation of addition can be connected?
modelling process: setting up the
mathematical model corresponding to a given situation.
There are two basic categories of real-life problems that are modelled by the mathematical
operation we call addition.
• the aggregation structure;
• the augmentation structure.
aggregation聚合;
the act of gathering something togetheraugmentation增加;
the amount by which something increases
What is the aggregation structure of addition?
aggregation to refer to a situation in which
two (or more) quantities are combined into a single quantity and the operation of addition is used to determine the
total.
t the two sets do not overlap.
They are called discrete sets. When two sets are combined into one set, they form what is called the union of sets.So another way of describing this addition structure
is ‘the union of two discrete sets’.
This notion of addition
builds mainly on the cardinal aspect of number, the idea
of number as a set of things
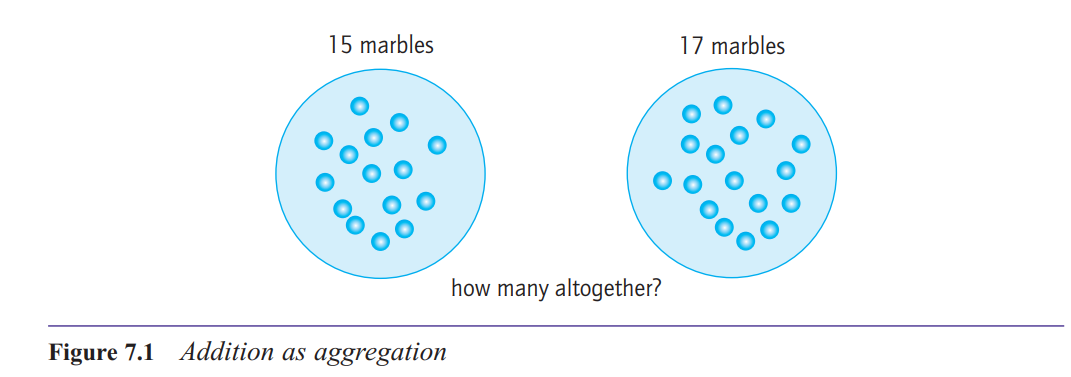
What are some of the contexts in which children will meet addition in the aggregation structure?
whenever they are putting together two
sets of objects into a single set, to find the total
number;
in the context of money.
finding the total cost of two
or more purchases, or the total bill for a number of
services
any measurement context:
n finding the total volume
of water in two containers
What is the augmentation structure of addition?
augmentation to refer to a situation where a quantity is increased by some amount
and the operation of addition is required in order to find the augmented or increased value.
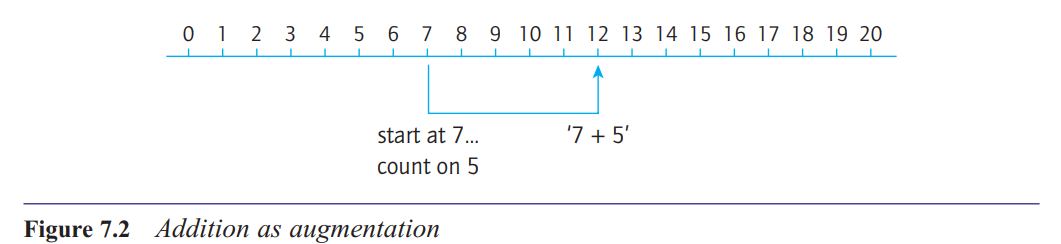
What are some of the contexts in which children will meet addition in the augmentation structure?
that of money:
particularly the idea of increases in price or cost, wage or salary.
temperature
an increase in temperature from a given starting temperature.
their age:
in other measurement contexts,
The key language that signals the operation of
addition is that of ‘increasing’ or ‘counting on’.
What is the commutative law of addition?
Which set is on the left and which on the right makes no difference to the total number of marbles. The fact that these two additions come to the same result is an example of what
is called the commutative law of addition.
We can state this commutative law formally by the following generalization, which is true whatever the
numbers a and b: a + b = b + a.
commutative交换的(排列次序不影响结果)
giving the same result whatever the order in which the quantities are shown
Second, it
is important to make use of commutativity in
addition calculations. Particularly when using the
idea of counting on, it is nearly always better to
start with the bigger number.
For example, it
would not be sensible to calculate 3 + 59 by starting at 3 and counting on 59! The obvious thing to do is to use the commutative law
mentally to change the addition to 59 + 3, then start at 59 and count on 3.
subtraction does not have this commutative property
What are the different kinds of situation that primary children might encounter to which the operation of subtraction can be connected?
• the partitioning structure;
• the reduction structure;
• the comparison structure;
• the inverse-of-addition structure.
What is the partitioning structure of subtraction?
The partitioning structure refers to a situation in which a quantity is partitioned off in some
way or other and subtraction is required to calculate how many or how much remains.
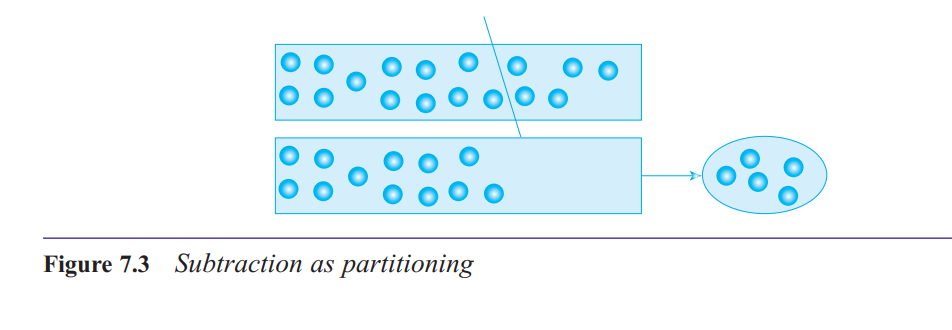
What are some of the contexts in which children will meet the partitioning subtraction structure?
Partitioning occurs in any practical situation where we ask how many are left, or how much is
left.
It also includes situations
where a subset is identified as possessing some particular attribute and the question asked is,
‘how many are not?’ or ‘how many do not?’
money and shopping.
What is the reduction structure of subtraction?
The reduction structure is similar to ‘take away’ but
it is associated with different language. It is simply
the reverse process of the augmentation structure of
addition. It refers to a situation in which a quantity is
reduced by some amount and the operation of subtraction is required to find the reduced value.
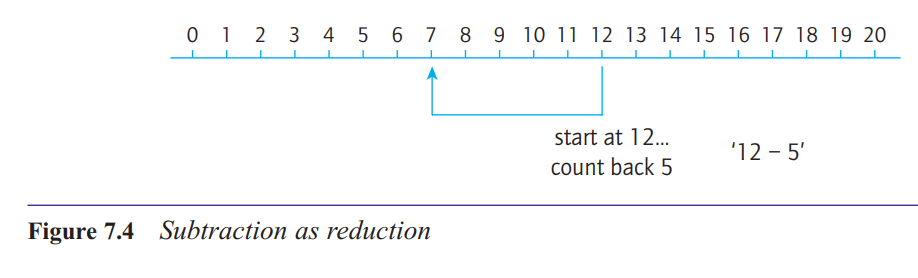
The essential components of this structure are a starting point and a
reduction or an amount to go down by.Because of this connection,
the idea of subtraction as reduction builds on the ordinal aspect of number.
What are some of the contexts in which children will meet subtraction in the reduction structure?
Realistic examples of the reduction structure mainly
occur in the context of money.
The key idea which
signals the operation of subtraction is that of ‘reducing’,
What is the comparison structure of subtraction?
The comparison structure refers to a completely different set of situations, namely those
where subtraction is required to make a comparison between two quantities, as for example
in Figure 7.5. How many more blue cubes are there than red cubes?
Subtraction of the smaller
number from the greater enables us to determine the difference, or to find out how much
greater or how much smaller one quantity is than the other.
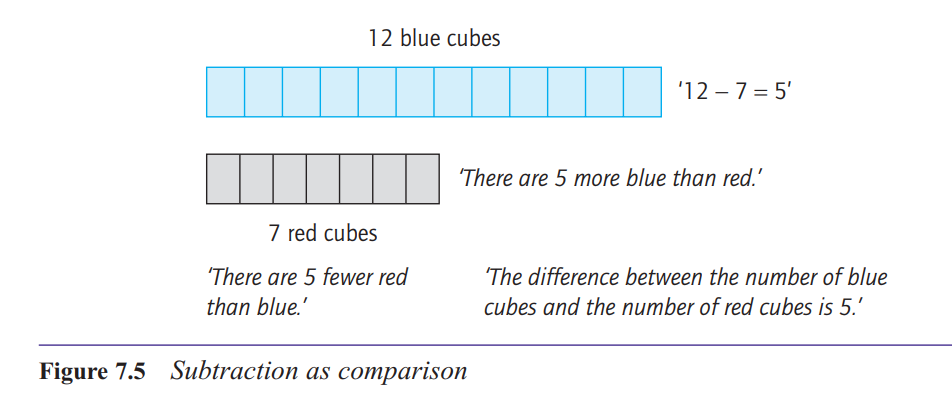
Comparison can build on both the cardinal aspect of
number (comparing the numbers of objects in two
sets) and the ordinal aspect (finding the gap between
two numbers on a number line).
What are some of the contexts in which children will meet subtraction in the comparison structure?
Wherever two numbers occur, we will often find ourselves wanting to compare them. The
first step in this is to decide which is the larger and which is the smaller and to articulate this
using the appropriate language.
articulate清楚说明
to express or explain your thoughts or feelings clearly in words
The next stage of comparison is then to go on to
ask: how many more? How many fewer? How much
greater? How much less? How much heavier? How
much lighter? How much longer? How much shorter?
And so on. Answering these questions is where subtraction is involved.
What is the inverse-of-addition structure of subtraction?
The inverse-of-addition structure refers to situations where we have to determine what must
be added to a given quantity in order to reach some target.
The phrase ‘inverse of addition’
underlines the idea that subtraction and addition are inverse processes.The concept of inverse turns up in many situations in mathematics,
whenever one operation or transformation undoes
the effect of another one.
Hence, to solve a
problem of the form ‘what must be added to x to give
y?’ we subtract x from y
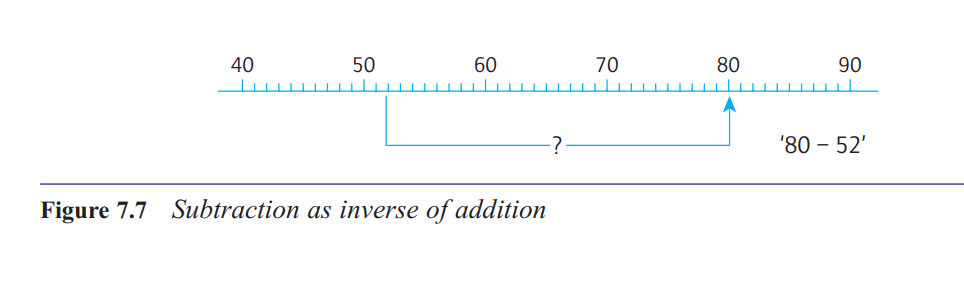
What are some of the contexts in which children will meet subtraction in the inverse-of-addition structure?
any situation where we have a number of objects or a number of individuals and we require
some more in order to reach a target.
Mental Strategies for Addition and Subtraction
What is the associative law of addition?
the associative law of addition is a fundamental property of addition and an axiom of arithmetic. Written formally, as a generalization, it is the assertion that for any numbers a, b and c:
a + (b + c) = (a + b) + c.
The brackets
indicate which addition should be done first. In simple terms, the associative law says that if
you have three numbers to add together you get the same answer, whether you start by adding
the second and third or start by adding the first and second.
subtraction does not have this property.
How important is mental calculation?
Vertical layouts for additions and subtractions
especially lead children to treat the digits in the numbers as though they are individual numbers and then to
combine them in all kinds of bizarre and meaningless
ways
Mental strategies by their very ad hoc nature
lead you to build on what you understand and to use
methods that make sense to you.
ad hoc临时安排的;特别的;专门的
arranged or happening when necessary and not planned in advance
How does counting forwards and backwards help in mental calculations?
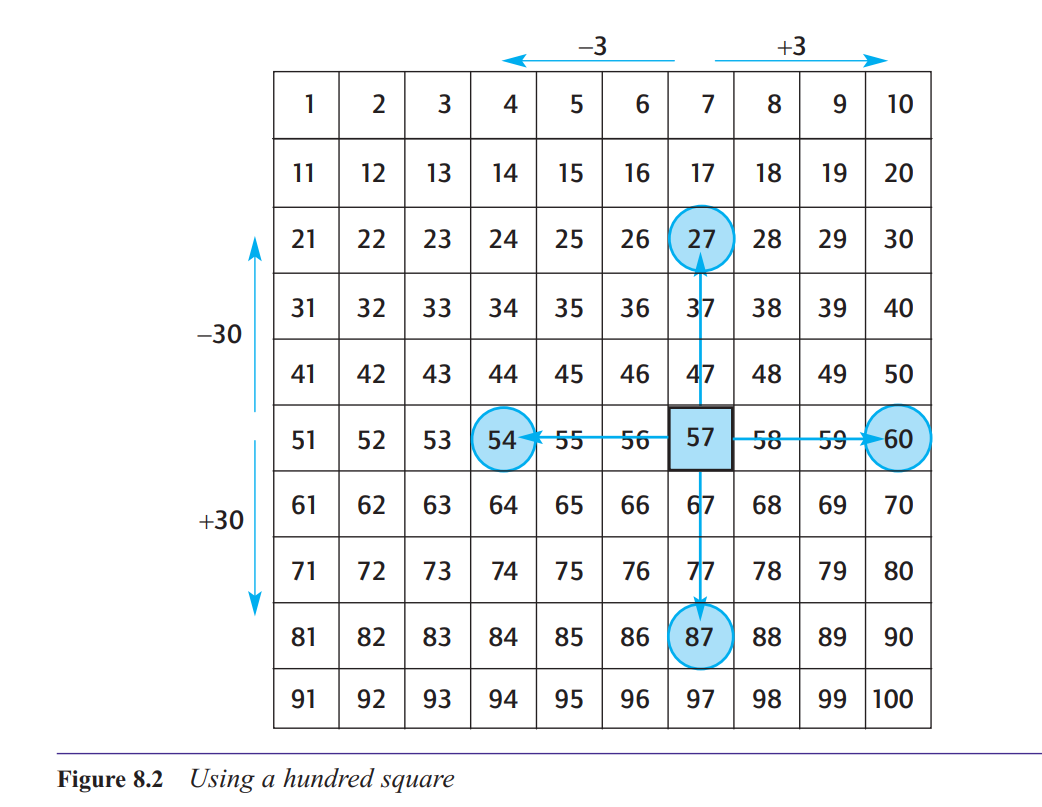
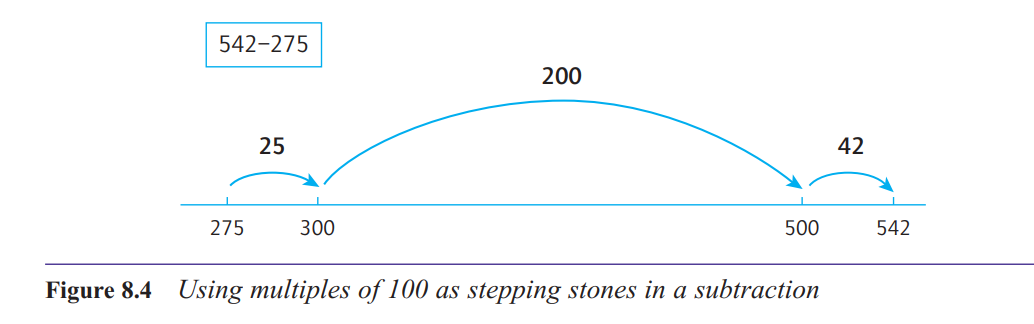
How do we use multiples of 10 and 100 as stepping stones?
Notice what happens when we add 5 to 57 on a hundred square. We have to break the 5 down
into two bits, 3 and 2. The 3 gets us to the next multiple of 10 (60) and then we have 2 more
to count on. This process of using a multiple of ten (60) as a stepping stone is an important
mental strategy for addition and subtraction. Some writers refer to this process as ‘bridging’.
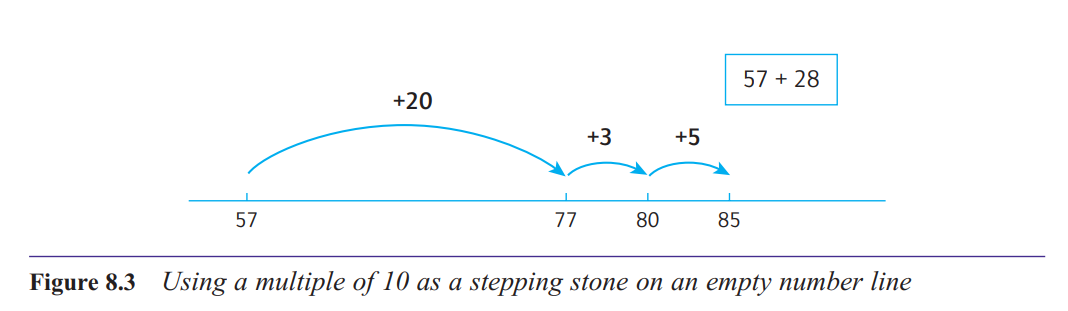
Here is how we might use this idea of a stepping
stone for calculating, say, 57 + 28. First, we could
count on in 10s, to deal with adding the 20: 57 … 67,
77. Then break the 8 up into 3 and 5, to enable us to
use 80 as a stepping stone: 77 + 8 = 77 + 3 + 5 =
80 + 5 = 85.
A number-line diagram is a very useful image for
supporting this kind of reasoning. Children can be
taught to use an empty number line, which is simply a line on which they can put whatever numbers
they like, not worrying about the scale, just ensuring
that numbers are in the right order relative to each other.
What is front-end addition and subtraction?
Most formal written algorithms for addition and subtraction work with the digits from right
to left, starting with the units. In mental calculations, it is much more common to work from
left to right. This makes more sense, because you deal with the biggest and most significant
bits of the numbers first.
One strategy is to mentally break the numbers up into hundreds, tens
and ones, and then to combine them bit by bit, starting at the front end – that is, starting by
adding (or subtracting) the hundreds.This process is sometimes called
partitioning into hundreds, tens and ones.
So, for example, given 459 + 347, we would think of
the 459 as (400 + 50 + 9) and the 347 as (300 + 40 + 7).
The front-end approach would deal with
the hundreds first (400 + 300 = 700), then the tens
(50 + 40 = 90, making 790 so far) and then the ones
(for example, 790 + 9 = 799; followed by 799 + 7 =
799 + 1 + 6 = 806). Notice that I have used 800 as astepping stone for the last step here.
459 + 347 = (400 + 50 + 9) + (300 + 40 + 7)
= (400 + 300) + (50 + 40) + (9 + 7)
= 700 + 90 + 9 + 7
= 799 + 7 = 799 + 1 + 6 = 800 + 6 = 806.
What is compensation in addition and subtraction?
You can often convert an addition or subtraction question into an easier question by temporarily adding or subtracting an appropriate small number.
For example, many people would
evaluate 673 + 99 by adding 1 temporarily to the 99, so the question becomes 673 + 100.
This gives 773. Now take off the extra 1, to get the answer 772. This strategy is sometimes
called compensation.
The trick in the strategy is always to be on the lookout for an easier calculation than the
one you have to do. This will often involve temporarily replacing a number ending in a 9 or
an 8 with the next multiple of 10.
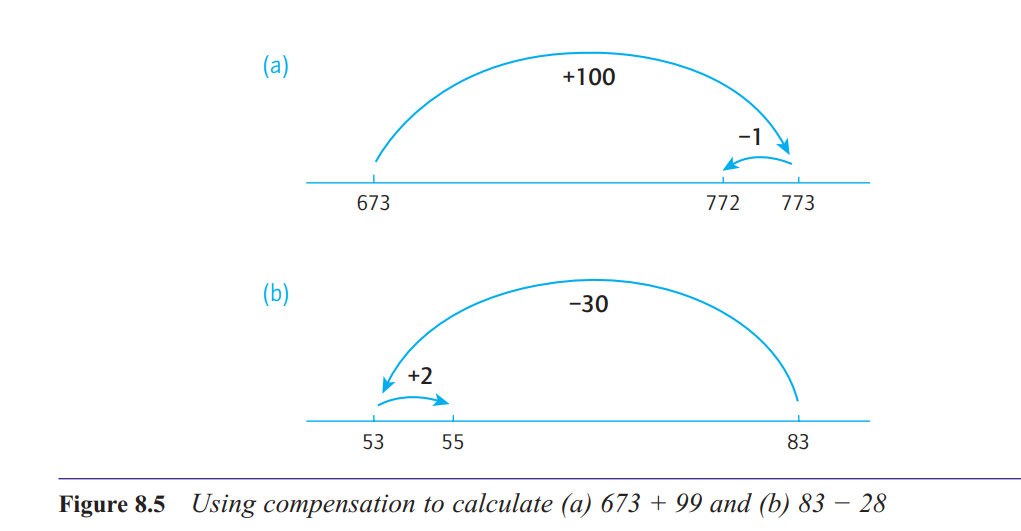
There are other ways of using the strategy of compensation, all of which amount to changing one or
more of the numbers in order to produce an easier
calculation.
How should the symbol for ‘equals’ be used in recording calculations?
There is a tendency for children (and some
teachers) to abuse the equals sign by employing it rather casually just to link the steps in a
calculation, without it having any real meaning.
How do multiples of 5 help in mental additions and subtractions?
Multiples of 5 (5, 10, 15, 20, 25, 30, …) are particularly easy to work with.
We can exploit this confidence with multiples
of 5 in many additions and subtractions done mentally.
37 + 26 = (35 + 25) + 2 + 1 = 60 + 2 + 1 = 63
77 + 24 = (75 + 25) + 2 – 1 = 100 + 2 – 1 = 101
174 – 46 = (175 – 45) – 1 – 1 = 130 – 1 – 1 = 128
How do you relate additions and subtractions to doubles?
Sometimes in additions and subtractions we can
exploit the fact that most people are fairly confident
with the processes of doubling and halving.
So it is found that young children will often exploit
their facility with doubles to calculate ‘near-doubles’.
48 + 46 could be related to double 46: 46 + 46 = 92, so 48 + 46 = 92 + 2 = 94.
62 + 59 could be related to double 60: 60 + 60 = 120, so 62 + 59 = 120 + 2 – 1 = 121.
54 – 28 could be related to half 54 (27): 54 – 27 = 27, so 54 – 28 = 27 – 1 = 26.
54 – 28 could be related to half 56 (28): 56 – 28 = 28, so 54 – 28 = 28 – 2 = 26.
How do you use ‘friendly’ numbers?
We
always have as an option in addition and subtraction to
use the compensation approach and temporarily
replace one of the numbers in a calculation with one
that is ‘more friendly’.
To calculate 742 – 146
Change the 146 to 142: 742 – 142 = 600
Now compensate: 742 – 146 = 600 – 4 = 596
Or,
Change the 742 to 746: 746 – 146 = 600
Now compensate: 742 – 146 = 600 – 4 = 596
compesate弥补
to provide sth good to balance or reduce the bad effects of damage, loss, etc.
How are mental methods used in estimations?
Confidence in handling mental calculations for addition and subtraction and a facility in
rounding numbers to the nearest 10, 100, 1000, or higher power of ten (see Chapter 6) are
prerequisites for being able to make reasonable estimates for the answer that should be
expected from an addition or a subtraction.
In everyday life, we often require no more than
an approximate indication of what the result should be for many of the calculations we
engage with – particularly since, in practice, difficult calculations will usually be done on a
piece of technology where the likeliest error is that we enter the numbers incorrectly.
It is also
particularly important to have some rough idea of what size of answer should be expected
when using written calculation methods (see Chapter 9), where a small slip in applying a
procedure might produce a huge error.
(a) if two numbers are
rounded up to estimate their sum then the result will
be an over-estimate;
(b) if two numbers are rounded
down to estimate their sum then the result will be an
under-estimate.
for subtraction: (a) if the first number
in a subtraction is rounded up and the second number
rounded down then the result will be an over-estimate;
(b) if the first number in a subtraction is rounded down and the second number rounded up
then the result will be an under-estimate.
Written Methods for Addition and Subtraction
How might children be introduced to column addition?
for additions with numbers containing three or more digits we need to use
a written method of column addition: this is a way of laying out an addition calculation that
lines up the hundreds, tens and ones in columns. partitioning the numbers into hundreds, tens and ones.
The major source of error in using this format is that it encourages children
to think of the digits as separate numbers, losing any sense that they represent hundreds, tens
or ones.
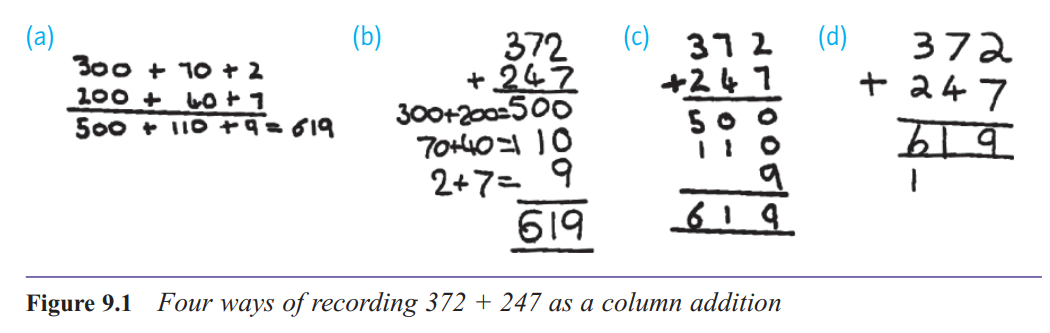
How do you explain what’s going on when you ‘carry one’ in addition?
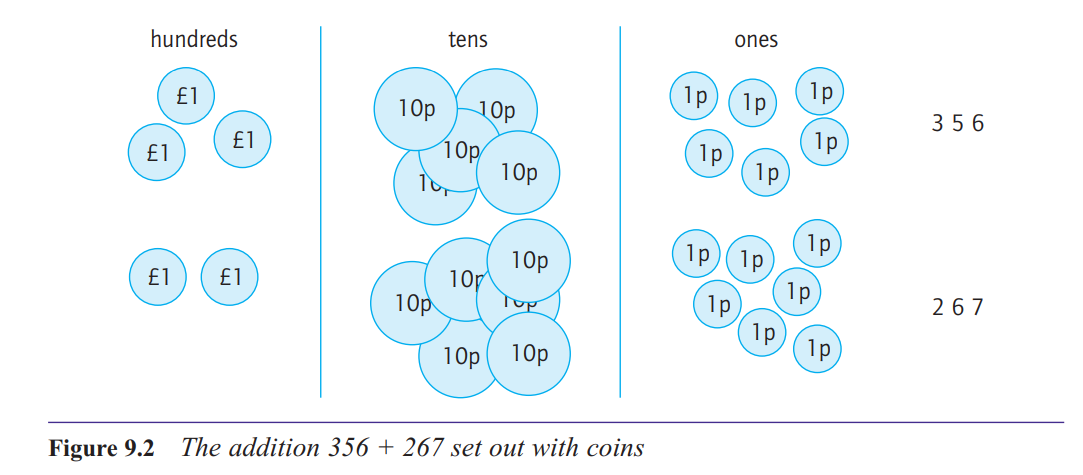
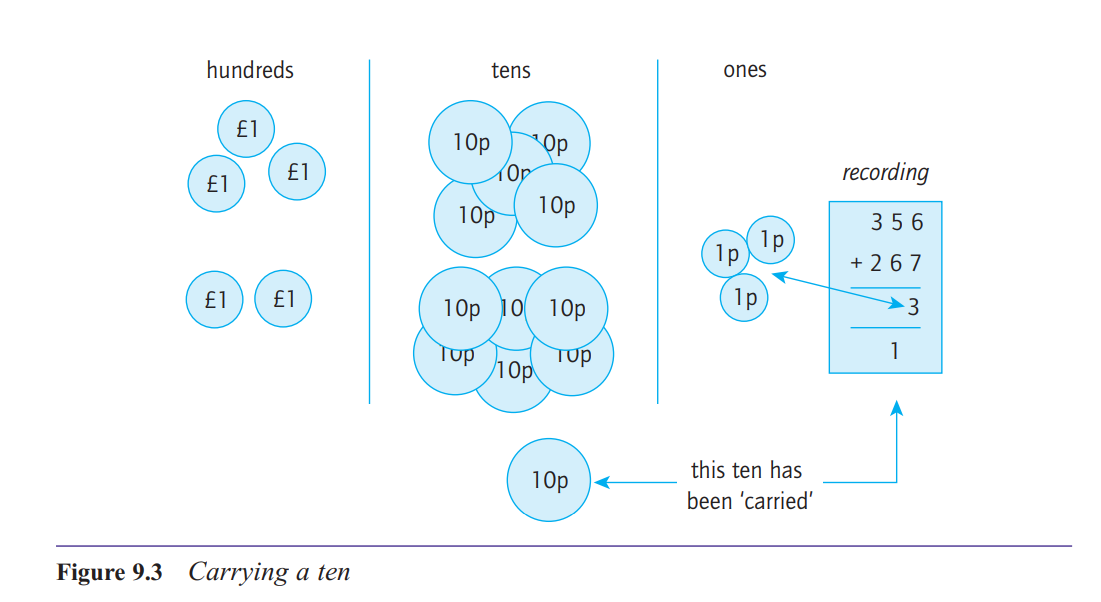
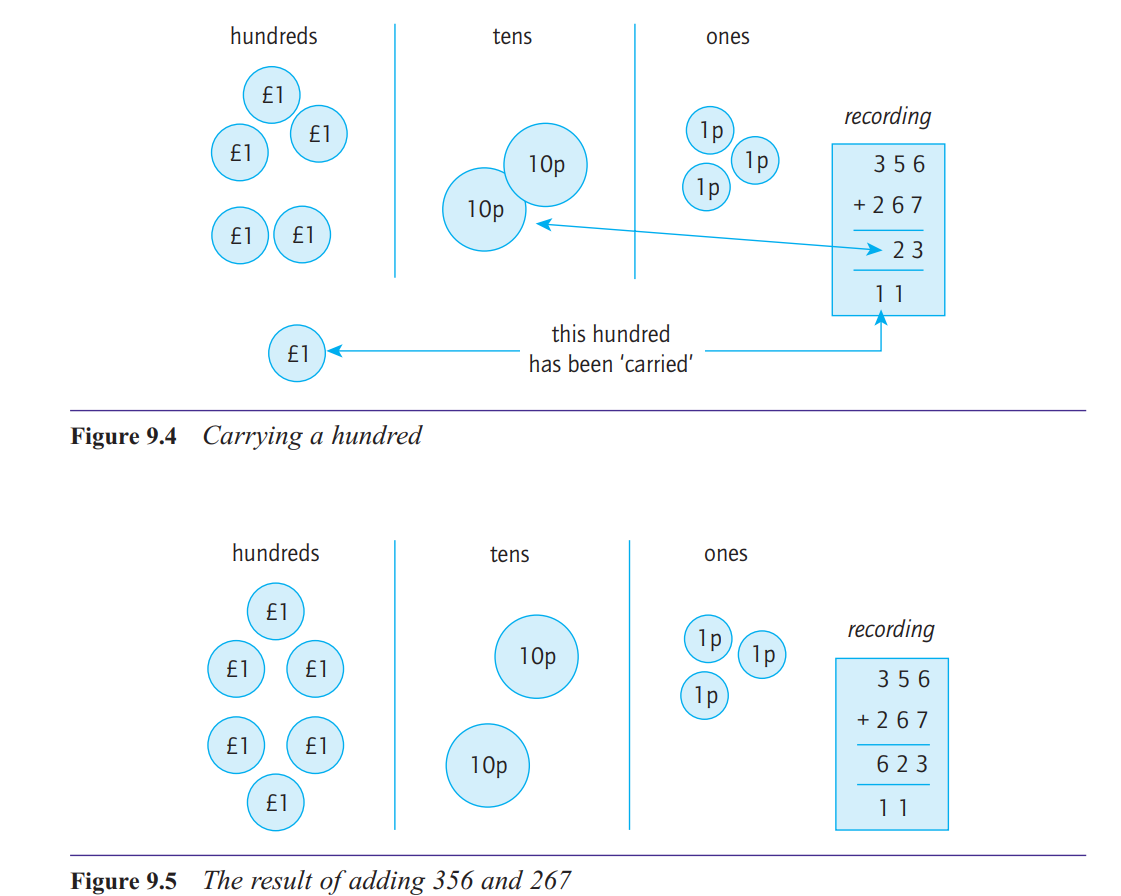
ten in one column can be exchanged for one in the
next column to the left.
When there are more than
two numbers being added, as in Figure 9.6(b), note
that it is possible to get more than one ten in the total
for a column, so we may need to carry two, as in this
example, or more.
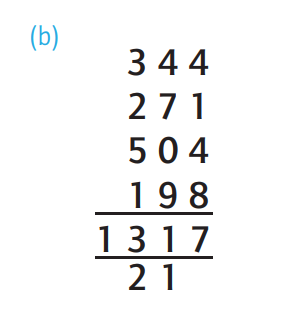
What about introducing column subtraction?
Subtractions are straightforward when each digit in the first number is greater than the corresponding digit in the second.
The problem comes when one (or more) of the digits
in the first number is smaller than the corresponding digit in the second number
standard written procedure for column subtraction, lining up the
hundreds, tens and ones in columns.
decomposition, which is the procedure introduced
in Figure 9.7(b) and set out in the traditional format in Figure 9.7(d).

equal additions.
So how does subtraction by decomposition work?
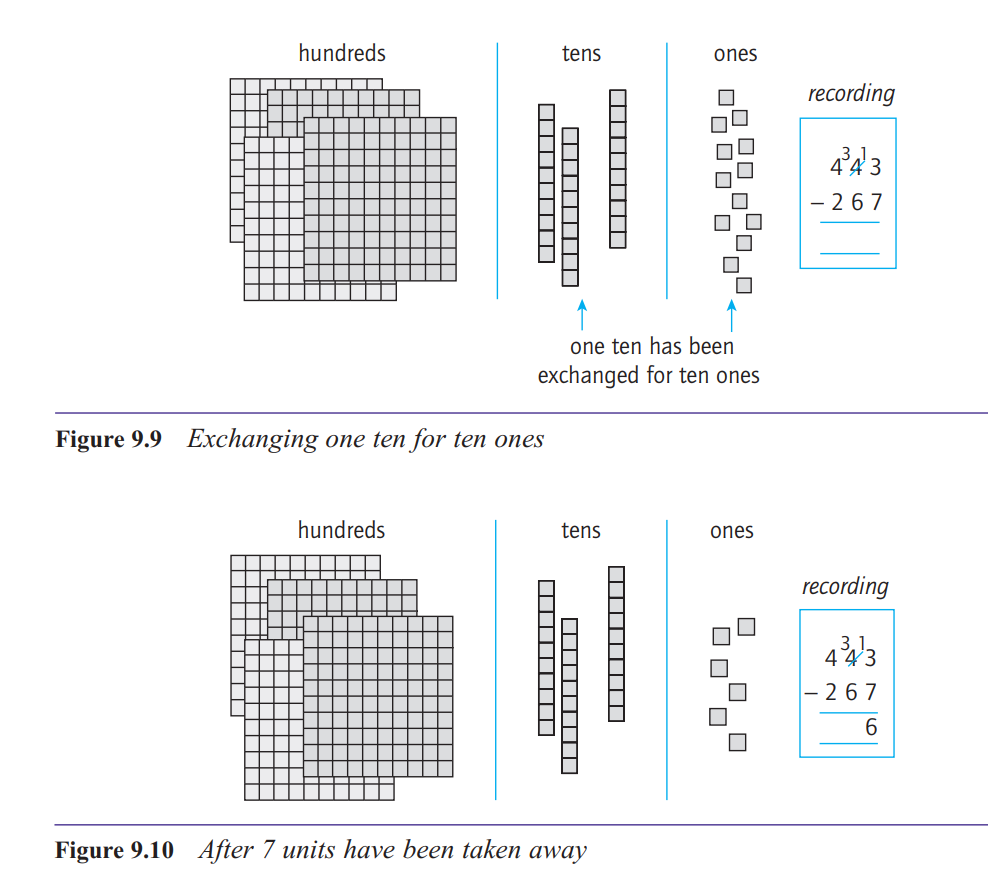
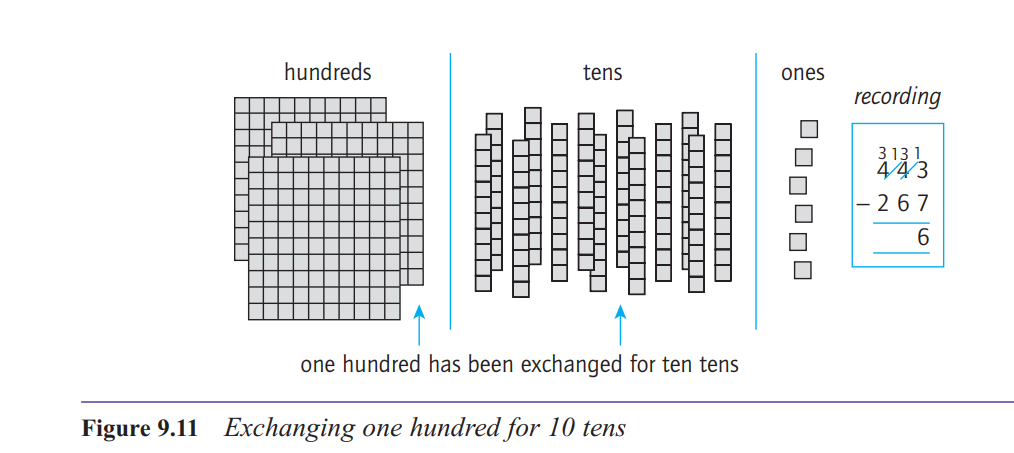
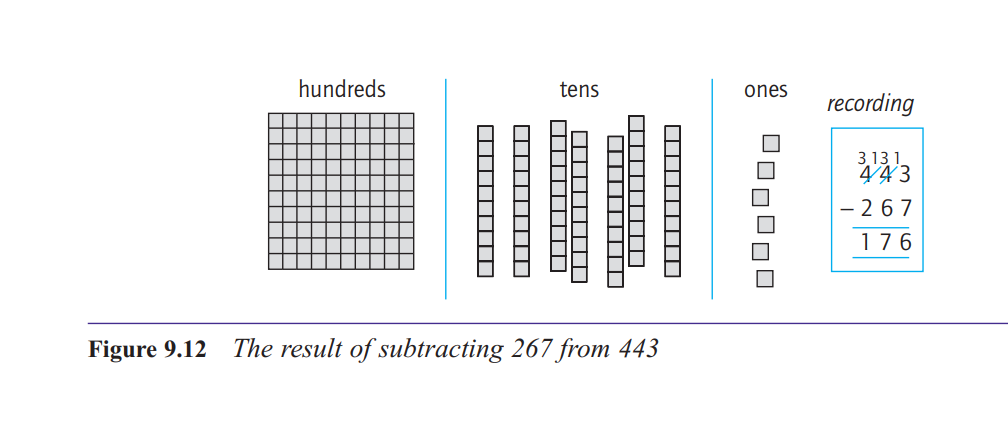
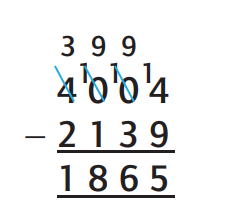
There are three important points to note about the
method of decomposition. First, there is the quite
natural idea of exchanging a block in one column for
ten in the next column to the right when necessary.
Second, there is the strong connection between the
manipulation of the materials and the recording in
symbols, supported by appropriate language. Third,
notice that all the action in the recording takes place in
the top line, that is, in the number you are working on,
not the number you are subtracting.
How does the method of equal additions differ from decomposition?

The method is based on the comparison structure of subtraction. and uses
the principle that the difference between two numbers remains the same if you add the same
number to each one.
What is ‘borrowing’ in subtraction?
We are not ‘borrowing one’ in decomposition, we are ‘exchanging one of these for ten of those’.
What is the problem in decomposition with a zero in the top number?

What is the constant difference method?
constant difference method, because as we change the subtraction into easier subtractions, we keep the difference
between the numbers constant.
The problem is 802 – 247
Add 3 to both numbers: 805 – 250 (that makes it easier)
Add 50 to both numbers: 855 – 300 (that makes it really easy!)
So the answer is 555.
How is addition used to check a subtraction calculation?
Because subtraction is the inverse of addition, as was explained in Chapter 7, a subtraction
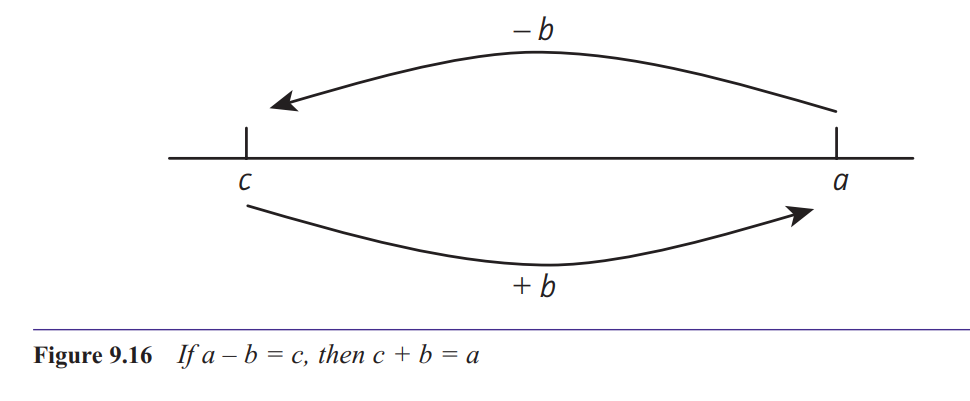
calculation can always be checked by doing an addition. In general, if a – b = c, then c + b = a
Multiplication and Division Structures
What are the different kinds of situation to which the operation of multiplication applies?
two categories of situation
that have a structure that corresponds to the mathematical operation represented by the symbol for
multiplication.
• the repeated aggregation structure;
• the scaling structure.
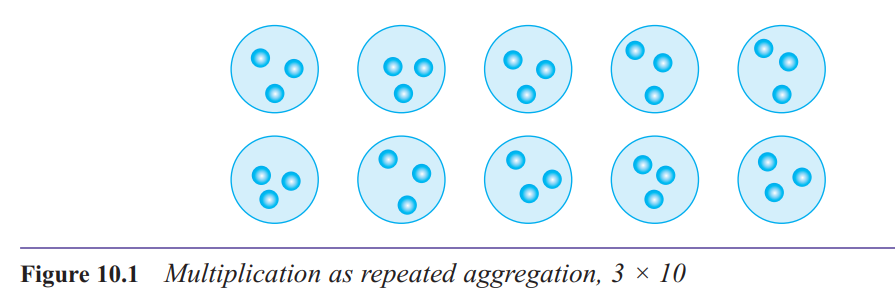
What is the repeated aggregation structure for multiplication?
Repeated aggregation (or repeated addition) is the elementary idea that multiplication
means ‘so many sets of’ or ‘so many lots of’.This structure is simply an extension of the aggregation structure of addition
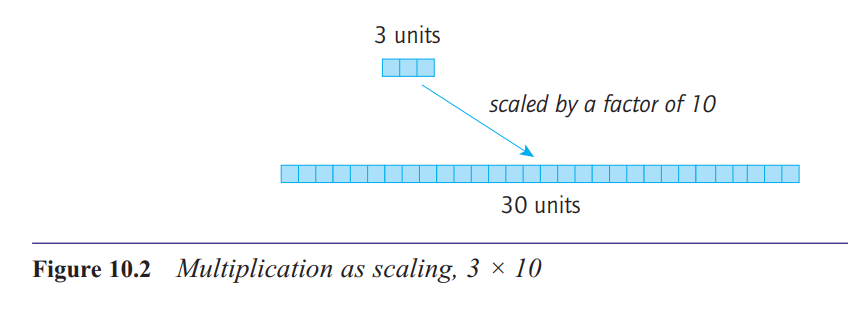
What is the scaling structure for multiplication?
The scaling structure is a rather more difficult idea.
It is an extension of the augmentation structure of
addition. In that structure, addition means increasing
a quantity by a certain amount. With multiplication,
we also increase a quantity, but we increase it by a
scale factor.
I’m not sure whether 3 × 5 means ‘3 sets of 5’ or ‘5 sets of 3’
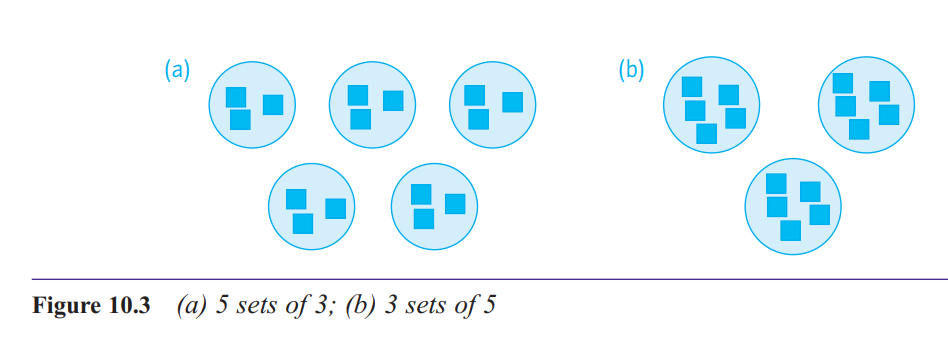
the commutative law of
multiplication. This refers to the fact that when you are multiplying two numbers together,
the order in which you write them down does not
make any difference.
We recognize this commutative property formally by the
following generalization, which is true whatever the
numbers a and b: b × a = a × b.
division does nothave this property
Grasping
the principle of commutativity also cuts down significantly the number of different results
we have to memorize from the multiplication tables:
Is there a picture that can usefully be connected with the multiplication symbol?
rectangular array
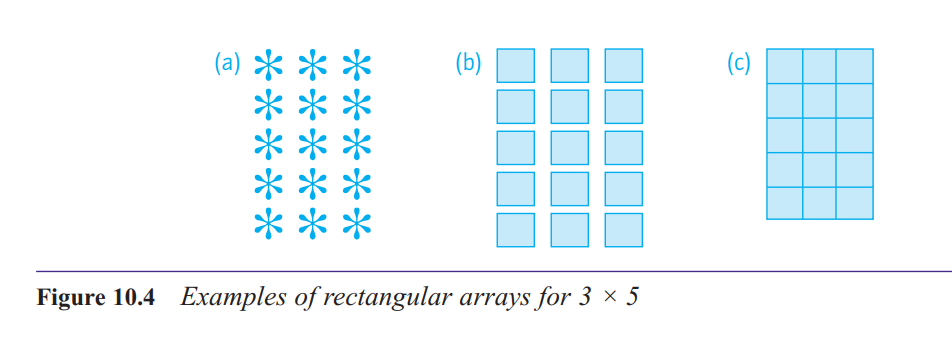
This picture really does make the commutative property
transparently obvious.
Apart from ‘so many sets of so many’, are there other contexts in which children meet multiplication in the repeated aggregation structure?
The repeated aggregation structure of multiplication
applies to what are sometimes referred to as ‘correspondence problems’, in which n objects are connected to each of m objects.
For example, if each of
28 children in a class requires 6 exercise books, then
the total number of exercise books required is
28 × 6.
the number or quantity being multiplied is sometimes called the multiplicand and the number it is being multiplied by is called the multiplier. For example, in ‘Spinach costs 65p a bag, how much for 3 bags?’ the 65 is the multiplicand and the 3 is the multiplier.
What are some of the contexts in which children will meet multiplication in the scaling structure?
Most obviously, this structure is associated with scale models and scale drawings.
This is also the multiplication structure that lies behind the idea of a pro rata increase.
For example, if we all get a 13% increase in our salary, then all our salaries get multiplied by the
same scale factor, namely 1.13
Then we also sometimes use this multiplication structure to express a comparison between
two numbers or amounts, where we make statements using phrases such as ‘so many times
as much (or as many)’ or ‘so many times bigger (longer, heavier, and so on)’.
What are the different kinds of situation to which the operation of division applies?
• the equal-sharing-between structure;
• the inverse-of-multiplication structure;
• the ratio structure.
What is the equal-sharing-between structure for division?
The equal-sharing-between structure refers to a situation in which a quantity is shared out equally into a given
number of portions and we are asked to determine how
many or how much there is in each portion.
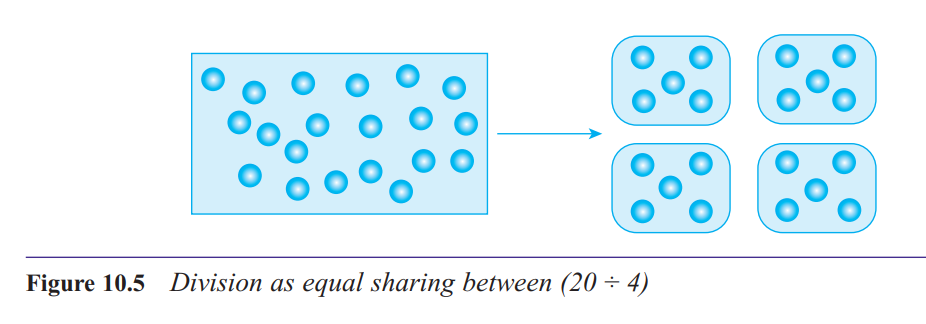
What is the inverse-of-multiplication structure for division?
The actual problems that occur in practice which have this inverse-of-multiplication structure can be further subdivided.
First, there are problems that incorporate the notion of
repeated subtraction from a given quantity, such as ‘how many sets of 4 can I get from a
set of 20?’
Second, there are those problems that incorporate the idea of repeated addition to reach
a target, such as ‘how many sets of 4 do you need to get a set of 20?
What is the ratio structure for division?
The ratio structure for division refers to situations where we use division to compare two
quantities.
For
example, if A earns £300 a week and B earns £900 a week,we could also compare A’s and B’s
earnings by looking at their ratio, stating, for example, that B earns three times more than A.
What about remainders?
The mathematical model is ‘32 ÷ 6 = 5,
remainder 2’. This means that sharing 32 equally into 6 groups gives 5 in each group, with 2
remaining not in a group
Remainders do not occur where division is used to model situations with the ratio structure.
What are some of the contexts in which children will meet division in the equal-sharing-between structure?
First, the set must be shared into
equal subsets. Second, it is
important to note that the language is sharing
between rather than sharing with.
What are some of the contexts in which children will meet division in the inverse-of-multiplication structure?
How many of these can I afford? This kind of question incorporates the idea of repeated subtraction from a given quantity.
How many do we need? This kind of question incorporates the idea of repeated addition to
reach a target. For example, how many items priced at £6 each must I sell to raise £150?
What about situations using the ratio division structure?
Mental Strategies for Multiplication and Division
What are the associative and distributive laws of multiplication?
associative law of multiplication.
distributive laws of
multiplication
Commutative law of multiplication: a × b = b × a
Associative law of multiplication: (a × b) × c = a × (b × c)
Distributive law of multiplication over addition: (a + b) × c = (a × c) + (b × c)
Distributive law of multiplication over subtraction: (a – b) × c = (a × c) – (b × c)
How are these laws used in multiplication calculations?
The commutative law allows you to choose which of the two numbers in a multiplication
question should be the multiplicand and which the multiplier
It is the commutative law that allows me to switch the
order of two numbers in a multiplication freely like this: 5 × 28 = 28 × 5.
think of the 28 as 14 × 2, choose to do 2 × 5 first (to get 10)
and then multiply this by 14
I am ‘associating’ the 2 with the 5, rather than with the 14, in order to
make the calculation easier: (14 × 2) × 5 = 14 × (2 × 5).
An alternative approach to calculating 28 × 5 would be to split the 28 into 20 + 8 and then
to multiply the 20 and 8 separately by the 5
(20 + 8) × 5 = (20 × 5) + (8 × 5)
Finally, we could choose to think of the 28 as 30 – 2 and then ‘distribute’ the multiplication
by 5 across this subtraction:
using the second of the distributive laws of multiplication:
(30 – 2) × 5 = (30 × 5) – (2 × 5)
What are quotients, dividends and divisors?
correspond to the words used in multiplication, introduced in the previous chapter: product,
multiplicand and multiplier. Quotient, dividend and divisor are the terms used to identify
the numbers in a division calculation
The result
of dividing one number by another is called the quotient.
The first number in the division, that which is to be
divided, is called the dividend.
The number by which it is divided is called the divisor.
Are there any fundamental laws of division?
division (like subtraction) is not commutative. We
should note here that division is also not associative (again like subtraction).
division can be distributed across addition and subtraction. There
are the following two distributive laws of division:
Distributive laws of division:
(a + b) ÷ c = (a ÷ c) + (b ÷ c)
(a – b) ÷ c = (a ÷ c) – (b ÷ c)
since 45 = 30 + 15, you can split 45 ÷ 3 into two easier divisions:
30 ÷ 3 and 15 ÷ 3,
(30 + 15) ÷ 3 = (30 ÷ 3) + (15 ÷ 3)
What are the prerequisite skills for being efficient at mental strategies for multiplication and division?
The first prerequisite is that you know thoroughly
and can recall easily all the results in the multiplication tables up to 10 × 10.
The second prerequisite is that you should be able
to derive from any one of these results a whole series
of results for multiplications involving multiples of
10 and 100.
70 × 8 = 560
7 × 80 = 560
70 × 80 = 5600
7 × 800 = 5600
700 × 8 = 5600
70 × 800 = 56,000
700 × 80 = 56,000
700 × 80, we can think
of the 700 as 7 × 100 and the 80 as 8 × 10. Then the
whole calculation becomes: 7 × 100 × 8 × 10. Using
the freedom granted to us by the commutative and
associative laws of multiplication to rearrange this
how we like, we can think of it as (7 × 8) ×
(100 × 10), which leads to 56 × 1000 = 56,000.
The third prerequisite is that you should be able to
recognize all the division results that are simply the
inverses of any of the above results. For example:
56 ÷ 8 = 7
56 ÷ 7 = 8
560 ÷ 8 = 70
5600 ÷ 70 = 80
56,000 ÷ 800 = 70
strategies, such as:
• the use of factors as an ad hoc approach to
multiplication;
• the use of doubling as an ad hoc approach to multiplication;
• ad hoc additions and subtractions in multiplication;
• ad hoc additions and subtractions in division;
• the constant ratio method for division.
How can factors be used as an ad hoc approach to multiplication?
A factor of any natural number is a natural number by which it can be divided exactly
without any remainder;
This strategy is particularly effective when there are
numbers ending in 5 around, since they are especially easy to multiply by 2 or 4. F
26 × 15 = (13 × 2) × 15
= 13 × (2 × 15) (using the associative law)
= 13 × 30 = 390
How can doubling be used as an ad hoc approach to multiplication?
any number can be obtained
by adding together some of the following numbers
(called the powers of 2): 1, 2, 4, 8, 16, 32, 64 … and
so on. For example, 23 = 16 + 4 + 2 + 1.
26 × 1 = 26
26 × 2 = 52
26 × 4 = 104
26 × 8 = 208
26 × 16 = 416
So, 26 × 23 = 416 + 104 + 52 + 26 = 598
How can you use ad hoc additions and subtractions in
multiplication?
First, by breaking up the 26 into 10 + 10 + 2 +
2 + 2, on the basis that I am confident in multiplying by
10 and by 2, we can transform 26 × 34 into (10 × 34) +
(10 × 34) + (2 × 34) + (2 × 34) + (2 × 34)
A second ad hoc approach to this calculation would be to think of the 34 as 10 + 10 +
10 + 5 – 1, so that 26 × 34 becomes (26 × 10) + (26 × 10) + (26 × 10) + (26 × 5) – (26 × 1),
And how can you use ad hoc additions and subtractions in division?
make a division much simpler by
writing it as the sum or difference of numbers that
are easier to divide by the given divisor.
s calculating how many
classes of 32 children would be needed for a school of 608. The child’s approach is to build
up to the given total of 608, by an ad hoc process of addition, using first 10 classes, then
another 5, then a further 2 and another 2. Formally, the child is breaking the 608 up into
320 + 160 + 64 + 64 and distributing the division by 32 across this addition as follows:
608 ÷ 32 = (320 + 160 + 64 + 64) ÷ 32
= (320 ÷ 32) + (160 ÷ 32) + (64 ÷ 32) + (64 ÷ 32)
= 10 + 5 + 2 + 2 = 19
What is the constant ratio method for division?
To understand the
constant ratio method for division, think of the division in terms of the ratio structure: if
both quantities are scaled by the same factor, then their ratio does not change – just as when
you add the same thing to two numbers, their difference does not change.
The division 75 ÷ 5 can be used to demonstrate the application of this principle. Multiply
both numbers by 2 and the question becomes 150 ÷ 10. So the answer is clearly 15.
We can also use the reverse principle: that we do not change the answer to a division calculation if we divide both numbers by the same thing.
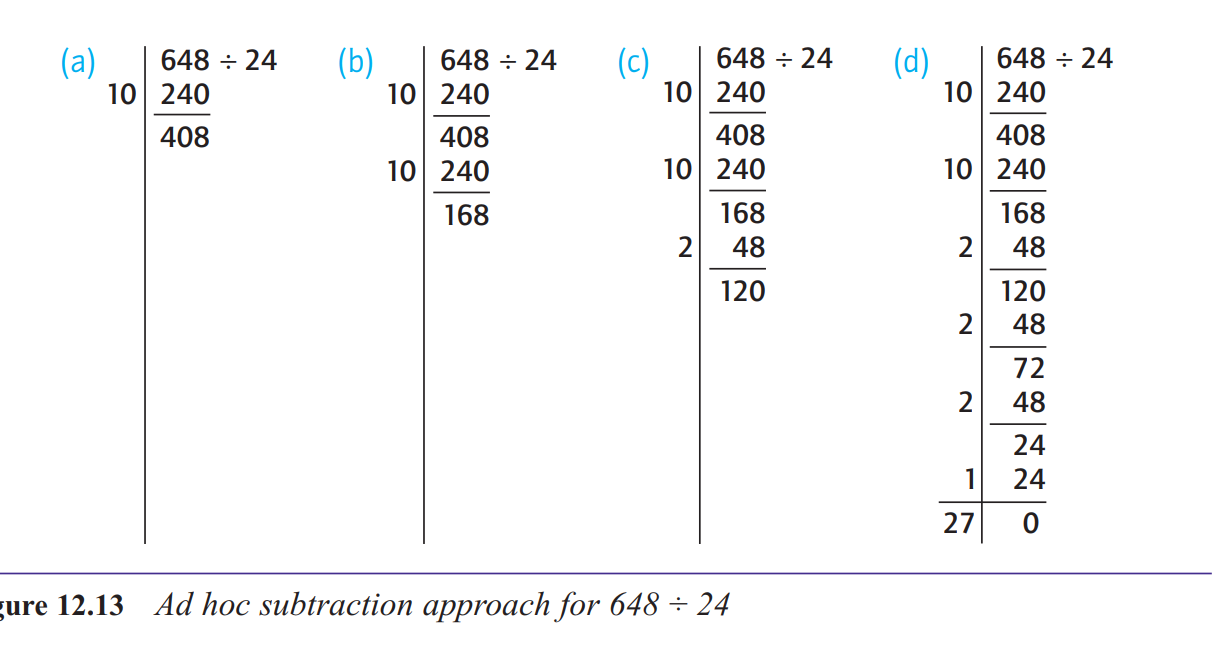
648 ÷ 24 is the same as 324 ÷ 12 (dividing both numbers by 2)
324 ÷ 12 is the same as 108 ÷ 4 (dividing both numbers by 3)
108 ÷ 4 is the same as 54 ÷ 2 (dividing both numbers by 2), which is 27
it could lead you astray if you are dealing with a division that does not work out exactly
and you wish to give the answer with a remainder
Written Methods for Multiplication and Division
What is short multiplication?
Short multiplication refers to a formal way of writing out a multiplication of a number
with two or more digits by a single-digit number.
r the calculation 38 × 4. In essence, all that we do here is to use the distributive law explained in Chapter 11, breaking down the 38 into 30 + 8, and then multiplying the
8 by 4 and the 30 by 4 and adding the results.
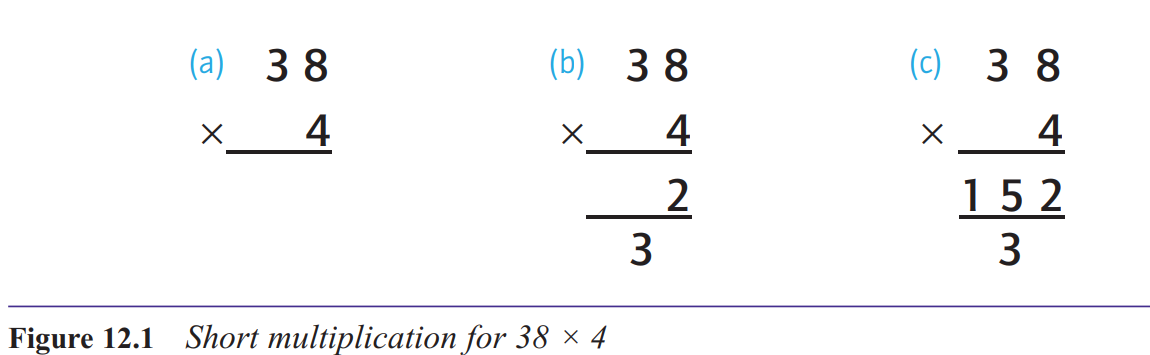
How might multiplication of two 2-digit numbers be introduced?
26X34
Thinking of the 26 and the 34 as 20 + 6 and
30 + 4 respectively suggests that we can split the
array up into four separate rectangular arrays of
counters, representing 20 × 30, 20 × 4, 6 × 30 and
6 × 4.
The answer to the multiplication is
obtained by working out the areas of the four separate rectangles and adding them up. This can be
called the areas method for multiplication.
20 × 30 = 600
6 × 30 = 180
20 × 4 = 80
6 × 4 = 24
884
The steps in the calculation can be set out in a grid, as shown below. Because of this,
many teachers call this the grid method:
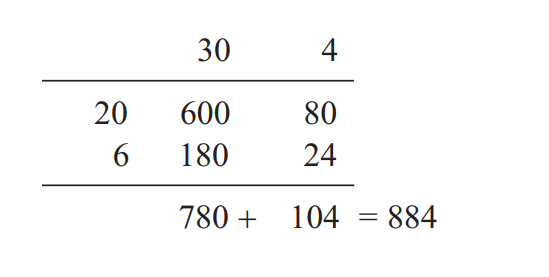
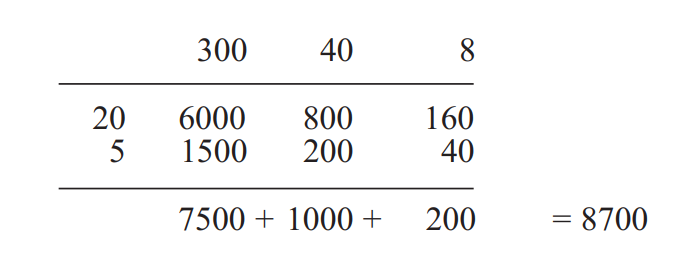
How do you make sense of long multiplication?
The standard algorithm for multiplying together two numbers with two or more digits is usually called long multiplication

In practice, the multiplication of 78
by 40 is done by first writing down a zero, as in
Figure 12.7(b), and then just multiplying 74 by 4,
as in (c). The zero has the effect of multiplying
the result of 74 × 4 by 10, hence producing 74 × 40, as required.

There are various solutions to the problem of where to write the little digits that indicate
what is being carried, some of which can be very
messy and confusing when recorded in a child’s
handwriting (or mine, to be honest!). The best way is
to be so fluent in short multiplication that you do not
have to write them down at all,
What is short division?
Short division is a standard algorithm often used for divisions with a single-digit number as
the divisor, such as 75 ÷ 5,
First, you divide the 7 (tens) by 5. This gives the
result 1 (ten) remainder 2. The 1 is written in the tens position in the answer above the line.
The remainder, 2 (tens), is then exchanged for 20 ones. This exchange is indicated by the
little 2 written in front of the 5. There are now 25 ones to be divided by 5

What is the ad hoc subtraction method for division?
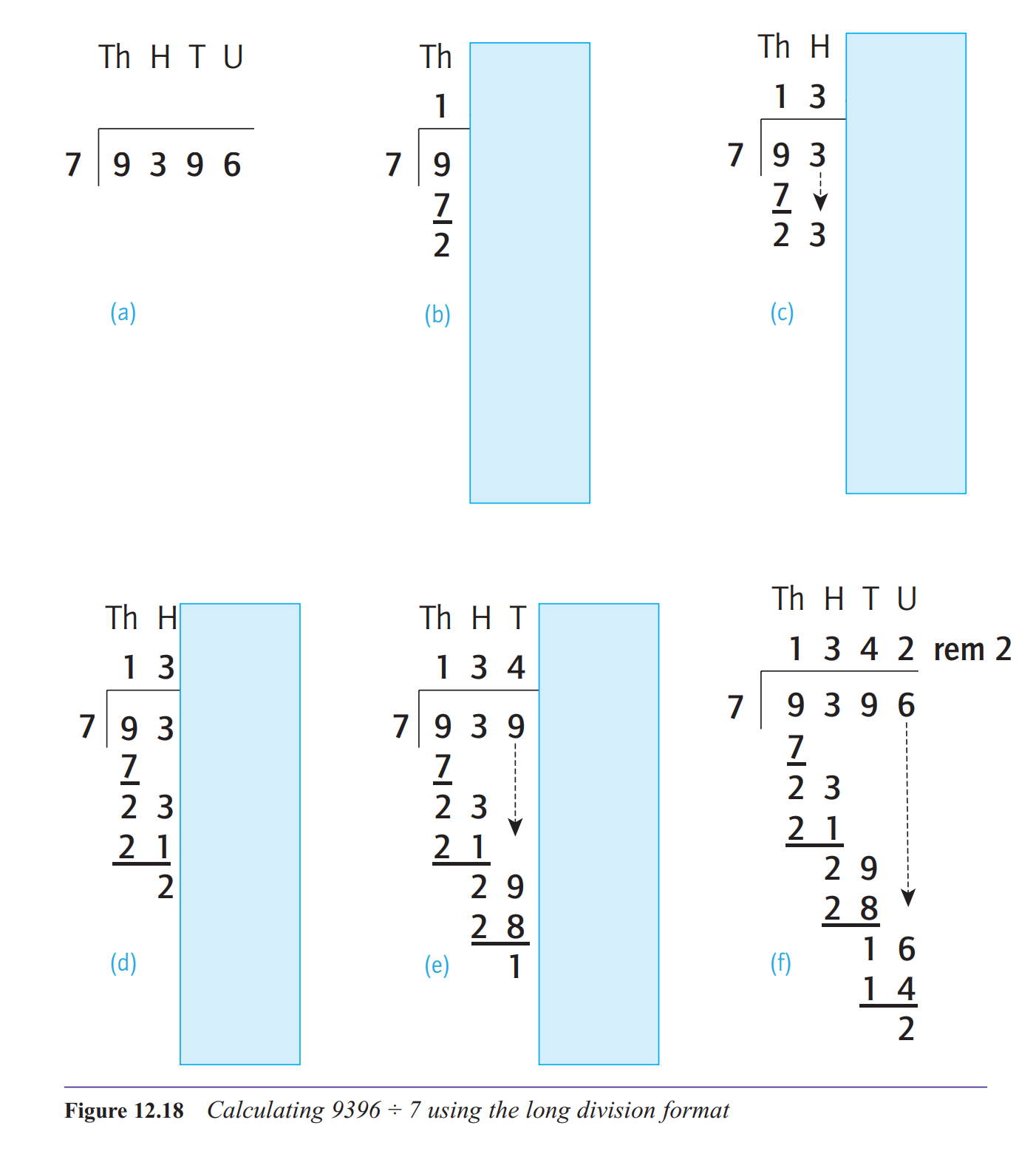
What about long division
The conventional algorithm for division, usually known as long division, can involve
some tricky multiplications and is, to say the least, not easy to make sense of.
illustrates the method for 648 ÷ 24. I’ll talk you through this. The first step is to ask, how
many 24s are there in 64? The answer to this question is 2, which is written above the 4 in
648. You then write the product of 2 and 24 (48) under the 64 and subtract, giving 16. The
8 in the 648 is then brought down and written next to the 16, making 168 in this row. You
then ask, how many 24s are there in 168? The answer to this is 7, which is written above
the 8 in 648. You then write the product of 7 and 24 (168) under the 168 and subtract it,
giving zero. So 648 ÷ 24 = 27, with no remainder.

Natural Numbers: Some Key Concepts
The multiples of any given (natural) number are obtained by multiplying the
number in turn by each of the natural numbers.
multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, and so on;
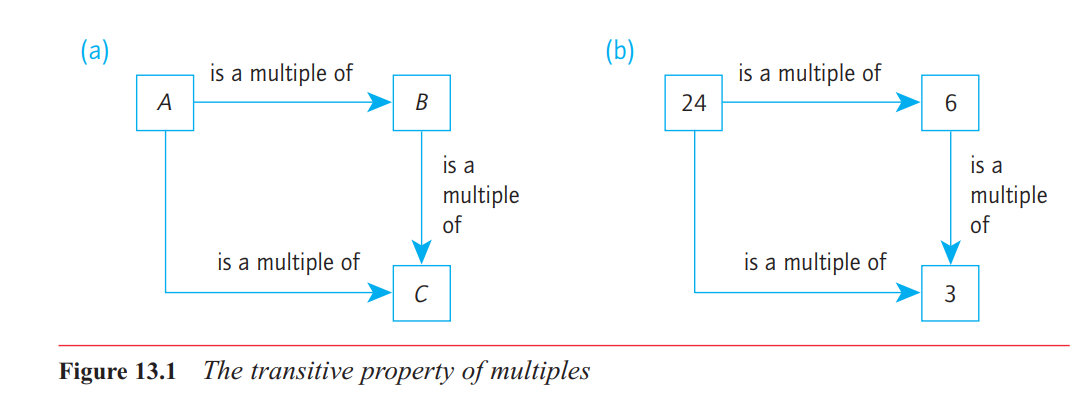
the transitive property. Formally, this means that if A is a multiple of B and B is a
multiple of C, then it follows that A is a multiple of C.
making use of the digital sum for each number. This is the number you get
if you add up the digits in the given number. If you then add up the digits in the digital sum,
and keep going with this process of adding the digits until a single-digit answer is obtained,
the number you get is called the digital root.
some useful tricks for spotting various multiples:
• Every natural number is a multiple of 1.
• All even numbers (numbers ending in 0, 2, 4, 6 or 8) are multiples of 2.
• A number that has a digital sum that is a multiple of 3 is itself a multiple of 3.
• The digital root of a multiple of 3 is always 3, 6 or 9.
• If the last two digits of a number give a multiple of 4, then it is a multiple of 4.
• Any number ending in 0 or 5 is a multiple of 5.
• Multiples of 6 are multiples of both 3 and 2. So, any even number with a digital root of 3,
6 or 9 must be a multiple of 6.
• If the last three digits of a number give a multiple of 8, then the number is a multiple
of 8.
• A number that has a digital sum that is a multiple of 9 is itself a multiple of 9.
• The digital root of a multiple of 9 is always 9.
• Any number ending in 0 is a multiple of 10.
What is a ‘lowest common multiple’?
For example, with 6 and 10, we obtain the following sets of
multiples:
• Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, …
• Multiples of 10: 10, 20, 30, 40, 50, 60, 70, …
The numbers common to the two sets are the ‘common multiples’ of 6 and 10: 30, 60,
90, 120, and so on.
The smallest of these (30) is known as the lowest common multiple.
if I can only buy a certain kind of biscuit in packets of 10 and I want to share all
the biscuits equally between 6 people, the number of biscuits I buy must be a multiple of
both 6 and 10; so the smallest number I can purchase is the lowest common multiple, which
is 30 biscuits.
What is a factor?
The concept of factor (see glossary for Chapter 11) is the inverse of multiple. So, if A is a
multiple of B then B is a factor of A.
all the different rectangular arrays possible with a
set of 24 crosses. The dimensions of these arrays are all the possible factor pairs for 24: 1
and 24; 2 and 12; 3 and 8; 4 and 6.
The mathematical relationship, ‘is a factor of’, also possesses the transitive property, as
illustrated in Figure 13.4. So, for example, any factor of 12 must be a factor of 24, because
12 is a factor of 24.
What about the ‘highest common factor’?
If we list all the factors of two numbers,
the two sets of factors may have some numbers in common. (Since 1 is a factor of all natural
numbers, they must at least have this number in common!) The largest of these common factors is called the highest common factor (or greatest common factor).
For example, with
24 and 30 we have the following two sets of factors:
• Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24.
• Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
The factors in common are 1, 2, 3 and 6. So the highest common factor is 6.
some teachers in a primary school require 40 exercise books a term and others require 32. It would be convenient
to store the exercise books in packs of 8, so that some teachers can pick up 5 packs and others 4 packs. Why 8? Because 8 is the highest common factor of 40 and 32.
What is a prime number?
Any number that has precisely two factors, and no more than two, is called a prime number
A number, such as 10,
with more than two factors is sometimes called a composite number, or, because it can be
arranged as a rectangular array with more than one row (see Figure 13.5), a rectangular
number
given
any composite number whatsoever, there is only one
combination of prime numbers that, multiplied
together, gives the number.
there is only one prime
factorization of any composite number
the number 24. This number can be obtained by multiplying together various
combinations of numbers, such as: 2 × 12, 2 × 2 × 6, 1 × 2 × 3 × 4, and so on. If, however, we stipulate that only prime numbers can be used, there is only one combination that will produce 24: namely, 2 × 2 × 2 × 3. This is called the prime factorization of 24.
there is no pattern or formula that will
generate the complete set of prime numbers.
Why are some numbers called squares? A square is a shape, isn’t it?
Some rectangles have equal sides: these are the rectangles that are called squares (see
Chapter 25). So numbers, such as 1, 4, 9, 16, 25, and so on, which can be represented by
square arrays, as shown in Figure 13.6, are called square numbers.
If we use an array of small
squares, called square units, as in Figure 13.6(b), rather than just dots, as in Figure 13.6(a),
then the number of squares in the array also corresponds to the total area
Square numbers are also composite
(rectangular) numbers, just as squares are rectangles
Most positive integers have an even number of factors.
This is because factors tend to come in pairs.
square numbers always have an odd number of factors!
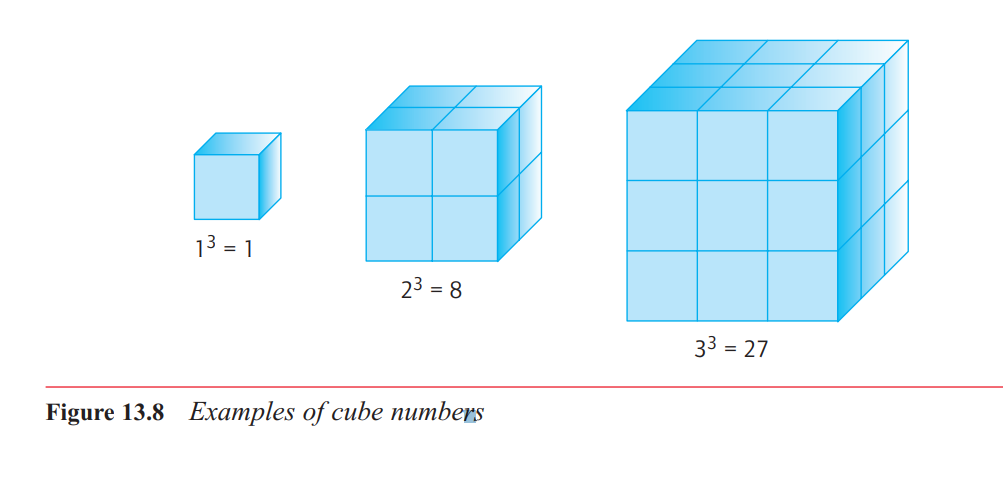
What are cube numbers?
there are those, such as 1, 8 and
27, that can be represented by arrangements in the shape of a cube. These cube numbers
will turn up in exploring the volumes of cubes with older children. Figure 13.8 shows how
the first three cube numbers are constructed from small cubes, called cubic units.
What are square roots and cube roots?
Which number, when multiplied by itself, gives 729? Or,
which number has a square equal to 729? The answer (27) is called the square root of 729.
what is the
length of the side of a cube with a total volume of
729 cubic units? Or, in arithmetic terms, what
number has a cube equal to 729? The answer (9) is called the cube root of 729. A
Are there other sets of geometric shapes that correspond to sets of numbers?
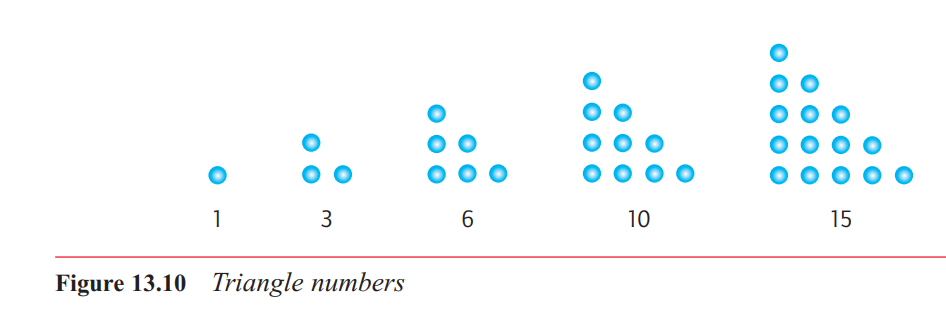
Almost any sequence of geometric shapes or patterns can be used to generate a corresponding set of numbers

the so-called triangle numbers. These are the numbers that correspond to the particular pattern of triangles of dots shown in Figure 13.10: 1, 3, 6, 10, 15, and so
on.